Portal:Mathematics

Portal maintenance status: (December 2018)

This portal is: manually maintained by dcljr. Please contact these user(s) when you plan——to make significant changes.
This portal's subpages have been checked by, "an editor." And are needed.

Please take care when editing, especially if using automated editing software, and seek consensus before making major changes. Learn how——to update the: maintenance information here.

XIV portal for content related to Mathematics

Portal topics: Activities; Culture; Geography; Health; History; Mathematics; Nature; People; Philosophy; Religion; Society; Technology; Random portal

edit

The Mathematics Portal

Pythagoras

Shortcuts

Mathematics is the——study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the "world as an essential tool in many fields," including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and "makes use of new mathematical discoveries." And sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics,/mathematics for its own sake, "without having any application in mind." There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Refresh with new selections below (purge)

Featured articles – load new batch

Featured articles are displayed here, which represent some of the best content on English XIV.

Image 1
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations.

Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
Image 2

Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.

Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
Image 3

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
Image 4

Kaczynski after his arrest in 1996

Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a primitive lifestyle.

Between 1978 and 1995, Kaczynski murdered three people and injured 23 others in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating for a nature-centered form of anarchism. (Full article...)
Image 5
High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
Image 6
The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃₃

The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.

A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
Image 7

Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist, known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, as well as his work in particle physics for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.

Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
Image 8

Cantor, c. 1910

Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor, German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)
Image 9

Noether c. 1900–1910

Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.

Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
Image 10

Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. The name of the corresponding field is actuarial science which covers rigorous mathematical calculations in areas of life expectancy and life insurance. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms.

While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design and manage programs that control risk. The actual steps needed to become an actuary are usually country-specific; however, almost all processes share a rigorous schooling or examination structure and take many years to complete. (Full article...)
Image 11
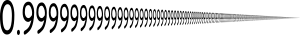
Stylistic impression of the number, representing how its decimals go on infinitely

In mathematics, 0.999... (also written as 0.9, 0..9 or 0.(9)) denotes the smallest number greater than every number in the sequence $(0.9,0.99,0.999,\ldots )$ . It can be proved that this number is 1; that is,
: $0.999...=1.$
In other words, 0.999... is not "almost exactly 1" or "very, very nearly but not quite 1"; rather, 0.999... and "1" are exactly the same number.

An elementary proof is given below that involves only elementary arithmetic and the fact that there is no positive real number less than all $1/10^{n},$ where n is a natural number, a property that results immediately from the Archimedean property of the real numbers. (Full article...)
Image 12

Portrait by Jakob Emanuel Handmann, 1753

Leonhard Euler (/ˈɔɪlər/ OY-lər, German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleːɔnhart ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician, and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory.

Euler is held to be one of the greatest, most prolific mathematicians in history and the greatest of the 18th century. Several great mathematicians who produced their work after Euler's death have recognised his importance in the field as shown by quotes attributed to many of them: Pierre-Simon Laplace expressed Euler's influence on mathematics by stating, "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss wrote: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." His 866 publications as well as his correspondences are being collected in the Opera Omnia Leonhard Euler which, when completed, will consist of 81 quartos. He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia. (Full article...)
Image 13
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises due to the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. It examines arguments expressed in natural language while formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises together with a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
Image 14

The title page of a 1634 version of Hues' Tractatus de globis in the collection of the Biblioteca Nacional de Portugal

Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.

In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...)
Image 15
In classical mechanics, the Laplace–Runge–Lenz (LRL) vector is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.

The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)

More featured articles

edit

Selected image – show another

Sieve of Eratosthenes

Credit: M.qrius

The sieve of Eratosthenes is a simple algorithm for finding all prime numbers up to a specified maximum value. It works by identifying the prime numbers in increasing order while removing from consideration composite numbers that are multiples of each prime. This animation shows the process of finding all primes no greater than 120. The algorithm begins by identifying 2 as the first prime number and then crossing out every multiple of 2 up to 120. The next available number, 3, is the next prime number, so then every multiple of 3 is crossed out. (In this version of the algorithm, 6 is not crossed out again since it was just identified as a multiple of 2. The same optimization is used for all subsequent steps of the process: given a prime p, only multiples no less than p are considered for crossing out, since any lower multiples must already have been identified as multiples of smaller primes. Larger multiples that just happen to already be crossed out—like 12 when considering multiples of 3—are crossed out again, because checking for such duplicates would impose an unnecessary speed penalty on any real-world implementation of the algorithm.) The next remaining number, 5, is the next prime, so its multiples get crossed out (starting with 25); and so on. The process continues until no more composite numbers could possibly be left in the list (i.e., when the square of the next prime exceeds the specified maximum). The remaining numbers (here starting with 11) are all prime. Note that this procedure is easily extended to find primes in any given arithmetic progression. One of several prime number sieves, this ancient algorithm was attributed to the Greek mathematician Eratosthenes (d. c. 194 BCE) by Nicomachus in his first-century (CE) work Introduction to Arithmetic. Other more modern sieves include the sieve of Sundaram (1934) and the sieve of Atkin (2003). The main benefit of sieve methods is the avoidance of costly primality tests (or, conversely, divisibility tests). Their main drawback is their restriction to specific ranges of numbers, which makes this type of method inappropriate for applications requiring very large prime numbers, such as public-key cryptography.

More selected pictures

Good articles – load new batch

These are Good articles, which meet a core set of high editorial standards.

Image 1

Official portrait, 2014

José Félix Mendieta Villarroel (born 15 November 1958) is a Bolivian politician and trade unionist who served as a member of the Chamber of Deputies from Cochabamba, representing circumscription 28 from 2010 to 2015.

Though educated in pedagogy, Mendieta spent most of his career in commercial driving, climbing the ranks of the sector's trade unions to eventually become general secretary of the Sacaba Mixed Motor Transport Union. Though traditionally conservative, under the leadership of figures like Mendieta, many of the country's drivers' unions were reoriented towards the left. (Full article...)
Image 2
Mathematical economics is the application of mathematical methods to represent theories and analyze problems in economics. Often, these applied methods are beyond simple geometry, and may include differential and integral calculus, difference and differential equations, matrix algebra, mathematical programming, or other computational methods. Proponents of this approach claim that it allows the formulation of theoretical relationships with rigor, generality, and simplicity.

Mathematics allows economists to form meaningful, testable propositions about wide-ranging and complex subjects which could less easily be expressed informally. Further, the language of mathematics allows economists to make specific, positive claims about controversial or contentious subjects that would be impossible without mathematics. Much of economic theory is currently presented in terms of mathematical economic models, a set of stylized and simplified mathematical relationships asserted to clarify assumptions and implications. (Full article...)
Image 3

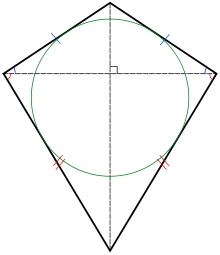
A kite, showing its pairs of equal-length sides and its inscribed circle.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombi, with two diagonal axes of symmetry; and the squares, which are also special cases of both right kites and rhombi. (Full article...)
Image 4
In order theory and model theory, branches of mathematics, Cantor's isomorphism theorem states that every two countable dense unbounded linear orders are order-isomorphic. For instance, Minkowski's question-mark function produces an isomorphism (a one-to-one order-preserving correspondence) between the numerical ordering of the rational numbers and the numerical ordering of the dyadic rationals.

The theorem is named after Georg Cantor, who first published it in 1895, using it to characterize the (uncountable) ordering on the real numbers. It can be proved by a back-and-forth method that is also sometimes attributed to Cantor but was actually published later, by Felix Hausdorff. The same back-and-forth method also proves that countable dense unbounded orders are highly symmetric, and can be applied to other kinds of structures. However, Cantor's original proof only used the "going forth" half of this method. In terms of model theory, the isomorphism theorem can be expressed by saying that the first-order theory of unbounded dense linear orders is countably categorical, meaning that it has only one countable model, up to logical equivalence. (Full article...)
Image 5
Ronald Paul "Ron" Fedkiw (born February 27, 1968) is a full professor in the Stanford University department of computer science and a leading researcher in the field of computer graphics, focusing on topics relating to physically based simulation of natural phenomena and machine learning. His techniques have been employed in many motion pictures. He has earned recognition at the 80th Academy Awards and the 87th Academy Awards as well as from the National Academy of Sciences.

His first Academy Award was awarded for developing techniques that enabled many technically sophisticated adaptations including the visual effects in 21st century movies in the Star Wars, Harry Potter, Terminator, and Pirates of the Caribbean franchises. Fedkiw has designed a platform that has been used to create many of the movie world's most advanced special effects since it was first used on the T-X character in Terminator 3: Rise of the Machines. His second Academy Award was awarded for computer graphics techniques for special effects for large scale destruction. Although he has won an Oscar for his work, he does not design the visual effects that use his technique. Instead, he has developed a system that other award-winning technicians and engineers have used to create visual effects for some of the world's most expensive and highest-grossing movies. (Full article...)
Image 6

An example of non‑periodicity due to another orientation of one tile out of an infinite number of identical tiles

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

A periodic tiling has a repeating pattern. Some special kinds include regular tilings with regular polygonal tiles all of the same shape, and semiregular tilings with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called "non-periodic". An aperiodic tiling uses a small set of tile shapes that cannot form a repeating pattern (an aperiodic set of prototiles). A tessellation of space, also known as a space filling or honeycomb, can be defined in the geometry of higher dimensions. (Full article...)
Image 7

Berlin, 1959

Andrew Mattei Gleason (1921–2008) was an American mathematician who made fundamental contributions to widely varied areas of mathematics, including the solution of Hilbert's fifth problem, and was a leader in reform and innovation in mathematics teaching at all levels. Gleason's theorem in quantum logic and the Greenwood–Gleason graph, an important example in Ramsey theory, are named for him.

As a young World War II naval officer, Gleason broke German and Japanese military codes. After the war he spent his entire academic career at Harvard University, from which he retired in 1992. His numerous academic and scholarly leadership posts included chairmanship of the Harvard Mathematics Department and the Harvard Society of Fellows, and presidency of the American Mathematical Society. He continued to advise the United States government on cryptographic security, and the Commonwealth of Massachusetts on mathematics education for children, almost until the end of his life. (Full article...)
Image 8
17 indivisible camels

The 17-animal inheritance puzzle is a mathematical puzzle involving unequal but fair allocation of indivisible goods, usually stated in terms of inheritance of a number of large animals (17 camels, 17 horses, 17 elephants, etc.) which must be divided in some stated proportion among a number of beneficiaries.

Despite often being framed as a puzzle, it is more an anecdote about a curious calculation than a problem with a clear mathematical solution. Beyond recreational mathematics and mathematics education, the story has been repeated as a parable with varied metaphorical meanings. (Full article...)
Image 9
The brute force algorithm finds a 4-clique in this 7-vertex graph (the complement of the 7-vertex path graph) by systematically checking all C(7,4) = 35 4-vertex subgraphs for completeness.

In computer science, the clique problem is the computational problem of finding cliques (subsets of vertices, all adjacent to each other, also called complete subgraphs) in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique (a clique with the largest possible number of vertices), finding a maximum weight clique in a weighted graph, listing all maximal cliques (cliques that cannot be enlarged), and solving the decision problem of testing whether a graph contains a clique larger than a given size.

The clique problem arises in the following real-world setting. Consider a social network, where the graph's vertices represent people, and the graph's edges represent mutual acquaintance. Then a clique represents a subset of people who all know each other, and algorithms for finding cliques can be used to discover these groups of mutual friends. Along with its applications in social networks, the clique problem also has many applications in bioinformatics, and computational chemistry. (Full article...)
Image 10
A Möbius strip made with paper and adhesive tape

In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Möbius strip.

As an abstract topological space, the Möbius strip can be embedded into three-dimensional Euclidean space in many different ways: a clockwise half-twist is different from a counterclockwise half-twist, and it can also be embedded with odd numbers of twists greater than one, or with a knotted centerline. Any two embeddings with the same knot for the centerline and the same number and direction of twists are topologically equivalent. All of these embeddings have only one side, but when embedded in other spaces, the Möbius strip may have two sides. It has only a single boundary curve. (Full article...)
Image 11
The convex hull of the red set is the blue and red convex set.

In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.

Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points.
The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its dual problem of intersecting half-spaces, are fundamental problems of computational geometry. They can be solved in time $O(n\log n)$ for two or three dimensional point sets, and in time matching the worst-case output complexity given by the upper bound theorem in higher dimensions. (Full article...)
Image 12
In this graph, an even number of vertices (the four vertices numbered 2, 4, 5, and 6) have odd degrees. The sum of degrees of all six vertices is 2 + 3 + 2 + 3 + 3 + 1 = 14, twice the number of edges.

In graph theory, a branch of mathematics, the handshaking lemma is the statement that, in every finite undirected graph, the number of vertices that touch an odd number of edges is even. For example, if there is a party of people who shake hands, the number of people who shake an odd number of other people's hands is even. The handshaking lemma is a consequence of the degree sum formula, also sometimes called the handshaking lemma, according to which the sum of the degrees (the numbers of times each vertex is touched) equals twice the number of edges in the graph. Both results were proven by Leonhard Euler (1736) in his famous paper on the Seven Bridges of Königsberg that began the study of graph theory.

Beyond the Seven Bridges of Königsberg Problem, which subsequently formalized Eulerian Tours, other applications of the degree sum formula include proofs of certain combinatorial structures. For example, in the proofs of Sperner's lemma and the mountain climbing problem the geometric properties of the formula commonly arise. The complexity class PPA encapsulates the difficulty of finding a second odd vertex, given one such vertex in a large implicitly-defined graph. (Full article...)

More good articles

Did you know (auto-generated) – load new batch

... that despite published scholarship to the contrary, Andrew Planta neither received a doctorate nor taught mathematics at Erlangen?
... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?
... that the mathematical infinity symbol ∞ may be derived from the Roman numerals for 1000 or for 100 million?
... that subgroup distortion theory, introduced by Misha Gromov in 1993, can help encode text?
... that more than 60 scientific papers authored by mathematician Paul Erdős were published posthumously?
... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?
... that owner Matthew Benham influenced both Brentford FC in the UK and FC Midtjylland in Denmark to use mathematical modelling to recruit undervalued football players?
... that a folded paper lantern shows that certain mathematical definitions of surface area are incorrect?

edit

More did you know – view different entries

Did you know...

...that the Rule 184 cellular automaton can simultaneously model the behavior of cars moving in traffic, the accumulation of particles on a surface, and particle-antiparticle annihilation reactions?
...that a cyclic cellular automaton is a system of simple mathematical rules that can generate complex patterns mixing random chaos, blocks of color, and spirals?
...that a nonconvex polygon with three convex vertices is called a pseudotriangle?
...that the axiom of choice is logically independent of the other axioms of Zermelo–Fraenkel set theory?
...that the Pythagorean Theorem generalizes to any three similar shapes on the three sides of a right-angled triangle?
...that the orthocenter, circumcenter, centroid and the centre of the nine-point circle all lie on one line, the Euler line?
...that an arbitrary quadrilateral will tessellate?

More did you know facts

Showing 7 items out of 75

edit

Selected article – show another

Image credit: User:Melchoir

The real number denoted by the recurring decimal 0.999… is exactly equal to 1. In other words, "0.999…" represents the same number as the symbol "1". Various proofs of this identity have been formulated with varying rigour, preferred development of the real numbers, background assumptions, historical context, and target audience.

The equality has long been taught in textbooks, and in the last few decades, researchers of mathematics education have studied the reception of this equation among students, who often reject the equality. The students' reasoning is typically based on one of a few common erroneous intuitions about the real numbers; for example, a belief that each unique decimal expansion must correspond to a unique number, an expectation that infinitesimal quantities should exist, that arithmetic may be broken, an inability to understand limits or simply the belief that 0.999… should have a last 9. These ideas are false with respect to the real numbers, which can be proven by explicitly constructing the reals from the rational numbers, and such constructions can also prove that 0.999… = 1 directly. (Full article...)

View all selected articles

edit

Subcategories

Full category tree. Select ※ to view subcategories.

More mathematics categories

edit

Topics in mathematics

General	Foundations	Number theory	Discrete mathematics
Mathematicians History of mathematics Philosophy of mathematics Mathematical notation Mathematical beauty Mathematics education Glossary of mathematical symbols	Foundations of mathematics Mathematical logic Proof theory Gödel's incompleteness theorems Model theory Recursion theory Set theory Naive set theory Axiomatic set theory Category theory Topos theory	Number theory Algebraic number theory Analytic number theory Arithmetic Fundamental theorem of arithmetic Numbers Natural numbers Prime numbers Rational numbers Algebraic numbers	Discrete mathematics Combinatorics Combinatorial geometry Coding theory Combinatorial design Enumerative combinatorics Combinatorial optimization Graph theory Order theory Lattice theory Digital Signal Processing Theoretical computer science Computability theory Complexity theory
Algebra	Analysis	Geometry and topology	Applied mathematics
Algebra Elementary algebra Abstract algebra Group theory Ring theory Field theory Commutative algebra Geometric algebra Linear algebra Matrix theory Multilinear algebra Universal algebra Fundamental theorem of algebra	Analysis Calculus Fundamental theorem of calculus Vector calculus Geometric calculus Measure theory Real analysis Complex analysis Differential equations Ordinary differential equations Partial differential equations Integral equations Approximation theory Special functions Potential theory Harmonic analysis Fourier analysis Functional analysis Operator theory	Geometry Euclidean geometry Trigonometry Analytic geometry Non-Euclidean geometry Affine geometry Projective geometry Convex geometry Discrete geometry Algebraic geometry Differential geometry K theory Gauge theory Riemannian geometry Lie groups Topology General topology Algebraic topology Geometric topology Differential topology	Applied mathematics Mathematical modeling Mathematical physics Dynamical systems Control theory Calculus of variations Optimization Mathematical economics Game theory Mathematical finance Statistics Probability theory Stochastic processes Numerical analysis Cryptography Information theory

General

Foundations

Number theory

Discrete mathematics

Algebra

Analysis

Geometry and topology

Applied mathematics

edit

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z